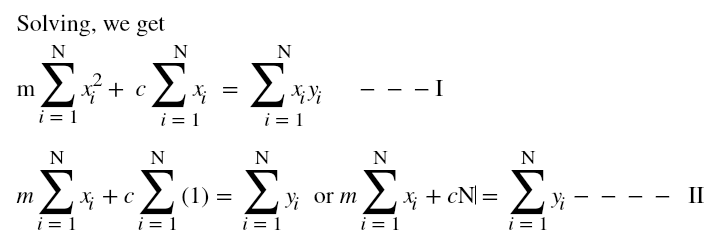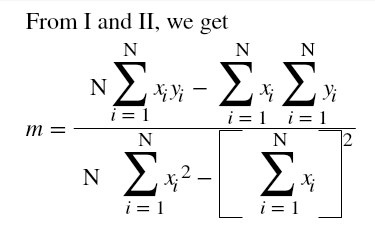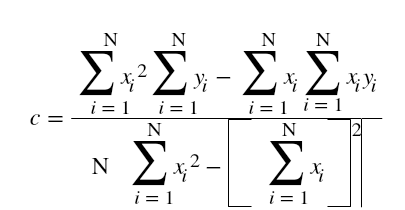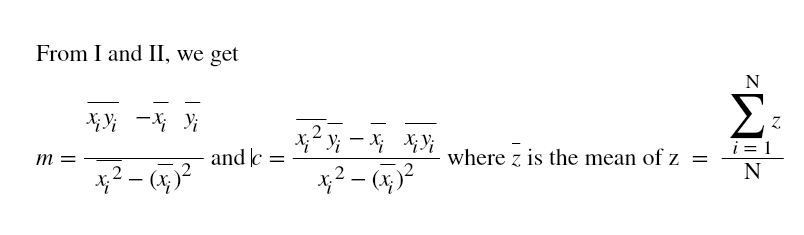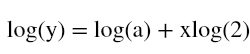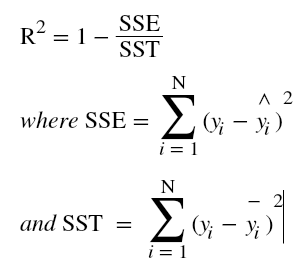Hi ML Enthusiasts! Today, We will be learning how to perform multivariate linear regression using R.
We will be using a very famous data set “
King County House sales” in which we will treat price as the dependent variable and other variables as independent variables. We will use these independent variables to predict the price of houses. Before going further, let’s know about our variables first.
The Dataset
In this data set, we have 19 house features and the number of observations being 21613.
–id: notation of the house
–date: date on which the house was sold
–price: price at which house was sold(target variable)
–bedrooms: number of bedrooms per house
–bathrooms: number of bathrooms per bedroom
–sqft_living: sqft footage of the home
–sqft_lot: sqft footage of the lot
–floors: total floors of the house
–waterfront: house which is having the waterfront view
–view: has been viewed
–condition: how good is the condition of the house
–grade: grade given to the house according to King County metrics
–sqft_above: apart from basement, sqft footage of the house
–yr_built: year in which the house was built
–yr_renovated: year in which house was renovated
–zipcode -lat: latitude coordinate
–long: longitude coordinate
–sqft_living15: living room area in 2015
–sqft_lot15: lot size area in 2015
Now, let’s read our csv file and store it in house dataframe and see if the data has any missing values.
house = read.csv('kc_house_data.csv')
summary(house)
## id date price
## Min. :1.000e+06 20140623T000000: 142 Min. : 75000
## 1st Qu.:2.123e+09 20140625T000000: 131 1st Qu.: 321950
## Median :3.905e+09 20140626T000000: 131 Median : 450000
## Mean :4.580e+09 20140708T000000: 127 Mean : 540088
## 3rd Qu.:7.309e+09 20150427T000000: 126 3rd Qu.: 645000
## Max. :9.900e+09 20150325T000000: 123 Max. :7700000
## (Other) :20833
## bedrooms bathrooms sqft_living sqft_lot
## Min. : 0.000 Min. :0.000 Min. : 290 Min. : 520
## 1st Qu.: 3.000 1st Qu.:1.750 1st Qu.: 1427 1st Qu.: 5040
## Median : 3.000 Median :2.250 Median : 1910 Median : 7618
## Mean : 3.371 Mean :2.115 Mean : 2080 Mean : 15107
## 3rd Qu.: 4.000 3rd Qu.:2.500 3rd Qu.: 2550 3rd Qu.: 10688
## Max. :33.000 Max. :8.000 Max. :13540 Max. :1651359
##
## floors waterfront view condition
## Min. :1.000 Min. :0.000000 Min. :0.0000 Min. :1.000
## 1st Qu.:1.000 1st Qu.:0.000000 1st Qu.:0.0000 1st Qu.:3.000
## Median :1.500 Median :0.000000 Median :0.0000 Median :3.000
## Mean :1.494 Mean :0.007542 Mean :0.2343 Mean :3.409
## 3rd Qu.:2.000 3rd Qu.:0.000000 3rd Qu.:0.0000 3rd Qu.:4.000
## Max. :3.500 Max. :1.000000 Max. :4.0000 Max. :5.000
##
## grade sqft_above sqft_basement yr_built
## Min. : 1.000 Min. : 290 Min. : 0.0 Min. :1900
## 1st Qu.: 7.000 1st Qu.:1190 1st Qu.: 0.0 1st Qu.:1951
## Median : 7.000 Median :1560 Median : 0.0 Median :1975
## Mean : 7.657 Mean :1788 Mean : 291.5 Mean :1971
## 3rd Qu.: 8.000 3rd Qu.:2210 3rd Qu.: 560.0 3rd Qu.:1997
## Max. :13.000 Max. :9410 Max. :4820.0 Max. :2015
##
## yr_renovated zipcode lat long
## Min. : 0.0 Min. :98001 Min. :47.16 Min. :-122.5
## 1st Qu.: 0.0 1st Qu.:98033 1st Qu.:47.47 1st Qu.:-122.3
## Median : 0.0 Median :98065 Median :47.57 Median :-122.2
## Mean : 84.4 Mean :98078 Mean :47.56 Mean :-122.2
## 3rd Qu.: 0.0 3rd Qu.:98118 3rd Qu.:47.68 3rd Qu.:-122.1
## Max. :2015.0 Max. :98199 Max. :47.78 Max. :-121.3
##
## sqft_living15 sqft_lot15
## Min. : 399 Min. : 651
## 1st Qu.:1490 1st Qu.: 5100
## Median :1840 Median : 7620
## Mean :1987 Mean : 12768
## 3rd Qu.:2360 3rd Qu.: 10083
## Max. :6210 Max. :871200
##
As can be seen from above details, there are no missing values, so there is no need to do missing value imputation. We can proceed towards our data relationship analysis. Now, let’s see how our data looks like by using the head() function.
head(house)
## id date price bedrooms bathrooms sqft_living
## 1 7129300520 20141013T000000 221900 3 1.00 1180
## 2 6414100192 20141209T000000 538000 3 2.25 2570
## 3 5631500400 20150225T000000 180000 2 1.00 770
## 4 2487200875 20141209T000000 604000 4 3.00 1960
## 5 1954400510 20150218T000000 510000 3 2.00 1680
## 6 7237550310 20140512T000000 1225000 4 4.50 5420
## sqft_lot floors waterfront view condition grade sqft_above sqft_basement
## 1 5650 1 0 0 3 7 1180 0
## 2 7242 2 0 0 3 7 2170 400
## 3 10000 1 0 0 3 6 770 0
## 4 5000 1 0 0 5 7 1050 910
## 5 8080 1 0 0 3 8 1680 0
## 6 101930 1 0 0 3 11 3890 1530
## yr_built yr_renovated zipcode lat long sqft_living15 sqft_lot15
## 1 1955 0 98178 47.5112 -122.257 1340 5650
## 2 1951 1991 98125 47.7210 -122.319 1690 7639
## 3 1933 0 98028 47.7379 -122.233 2720 8062
## 4 1965 0 98136 47.5208 -122.393 1360 5000
## 5 1987 0 98074 47.6168 -122.045 1800 7503
## 6 2001 0 98053 47.6561 -122.005 4760 101930
The date variable needs our attention here. It’s in incorrect format. Let’s convert it in a UTC format using lubridate library.
#The date may not be in character data type. So, we use as.character()
#in this case andsubset the date string with start=1 and stop = 8
house$date <- as.character(house$date)
house$date <- substr(house$date, 1, 8)
#Convert the date in year-month-date format
house$date <- as.Date(house$date, , format='%Y%m%d')
#Converting date into number of days with 1st jan 1900 as reference date
house$date <- as.numeric(as.Date(house$date, origin = "1900-01-01"))
head(house)
## id date price bedrooms bathrooms sqft_living sqft_lot floors
## 1 7129300520 16356 221900 3 1.00 1180 5650 1
## 2 6414100192 16413 538000 3 2.25 2570 7242 2
## 3 5631500400 16491 180000 2 1.00 770 10000 1
## 4 2487200875 16413 604000 4 3.00 1960 5000 1
## 5 1954400510 16484 510000 3 2.00 1680 8080 1
## 6 7237550310 16202 1225000 4 4.50 5420 101930 1
## waterfront view condition grade sqft_above sqft_basement yr_built
## 1 0 0 3 7 1180 0 1955
## 2 0 0 3 7 2170 400 1951
## 3 0 0 3 6 770 0 1933
## 4 0 0 5 7 1050 910 1965
## 5 0 0 3 8 1680 0 1987
## 6 0 0 3 11 3890 1530 2001
## yr_renovated zipcode lat long sqft_living15 sqft_lot15
## 1 0 98178 47.5112 -122.257 1340 5650
## 2 1991 98125 47.7210 -122.319 1690 7639
## 3 0 98028 47.7379 -122.233 2720 8062
## 4 0 98136 47.5208 -122.393 1360 5000
## 5 0 98074 47.6168 -122.045 1800 7503
## 6 0 98053 47.6561 -122.005 4760 101930
Our next step is to split the dataset into training and test data set. We do this by using the sample() function of R. We fix the ratio of training to test data as 80:20. So, we convert 0.2xdataset into test data and use the remaining, i.e., 0.8xdataset as training dataset.
splitRatio = sample(1:nrow(house), 0.2*nrow(house))
testHouseData = house[splitRatio,]
trainingHouseData = house[-splitRatio,]
Now comes the visualization part. Let’s look at how different variables are connected to price variable.
library(ggplot2)
library(GGally)
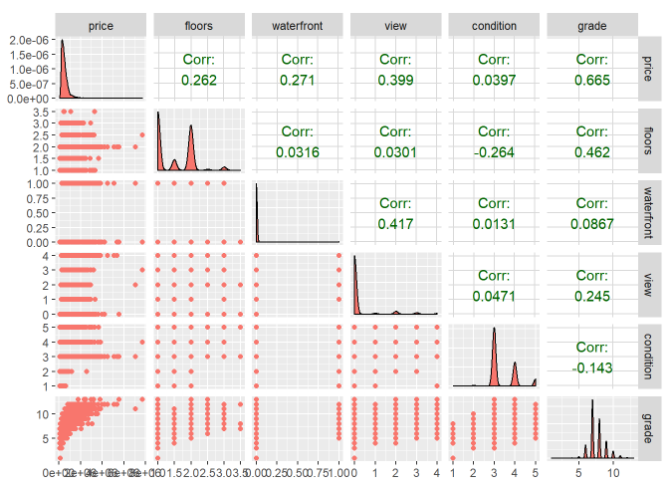
relPlot1 <- ggpairs(data = trainingHouseData,
columns = 3:7,
mapping = aes(color = "dark green"),
axisLabels = "show")
relPlot1

One thing to be noted above is that all the columns from 3 to 7 are having continuous numerical data. So, the columns = 3:7 has been fixed. After 7th column, all the columns from 8 to 12 are categorical in nature. So, we use columns = c(3, 8:12) with 3rd column(price) having continuous numerical data.
relPlot2 <- ggpairs(data = trainingHouseData,
columns = c(3, 8:12),
mapping = aes(color = "dark green"),
axisLabels = "show")
relPlot2
Let’s verify the relationship between columns 3, 15, 18 and 19.
relPlot3 <- ggpairs(data = trainingHouseData,
columns = c(3, 15, 18, 19),
mapping = aes(color = "dark green"),
axisLabels = "show")
relPlot3
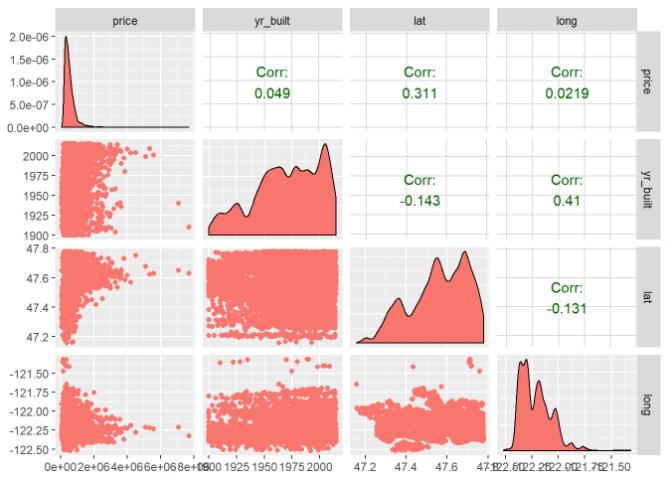
As you can see from the above plots, -corr between price vs sqft_living: 0.701 -corr between price vs bathrooms: 0.524 -corr between price vs grade: 0.654 -corr between price vs view: 0.406 -corr between price vs waterfront: 0.324 -corr between price vs lat: 0.304 -corr between price vs bedrooms: 0.303 -corr between price vs floors: 0.282 The correlation values between price and other variables are very small so that can be ignored as they are not posing any impact on the prices of the houses. Let’s now check the multi-collinearity among the variables using variance inflation factor concept.
library(car)
## Loading required package: carData
finalModel <- lm(price~sqft_living + bathrooms + grade + view + waterfront + bedrooms + floors, data=trainingHouseData)
vif(finalModel)
## sqft_living bathrooms grade view waterfront bedrooms
## 3.906712 2.858481 2.733885 1.321960 1.214251 1.609194
## floors
## 1.451042
Since all the vif values are less than 5, we can say that the model doesn’t have multicollinearity among the variables. So, we can consider all the variables of the said model.
step(finalModel)
## Start: AIC=427290.6
## price ~ sqft_living + bathrooms + grade + view + waterfront +
## bedrooms + floors
##
## Df Sum of Sq RSS AIC
## 9.3237e+14 427291
## - bathrooms 1 7.6493e+11 9.3314e+14 427303
## - floors 1 2.0967e+12 9.3447e+14 427327
## - bedrooms 1 7.3436e+12 9.3971e+14 427424
## - view 1 3.5588e+13 9.6796e+14 427936
## - waterfront 1 3.6058e+13 9.6843e+14 427945
## - grade 1 8.4533e+13 1.0169e+15 428789
## - sqft_living 1 1.3231e+14 1.0647e+15 429583
##
## Call:
## lm(formula = price ~ sqft_living + bathrooms + grade + view +
## waterfront + bedrooms + floors, data = trainingHouseData)
##
## Coefficients:
## (Intercept) sqft_living bathrooms grade view
## -468540.7 189.5 -14629.0 98753.5 68512.7
## waterfront bedrooms floors
## 561511.0 -27997.1 -24612.7
According to the above stats, our finalModel equation is price = 191.1(sqft_living) – 13159.1(bathrooms) + 98298.6(grade)+66911.4(view) +580801.6(waterfront) – 27495.8(bedrooms) – 27293.2(floors) – 467519.7. Let’s find out what is the value of R-square of this model by using summary() function.
summary(finalModel)
##
## Call:
## lm(formula = price ~ sqft_living + bathrooms + grade + view +
## waterfront + bedrooms + floors, data = trainingHouseData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1186479 -125387 -18824 95760 4742318
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.685e+05 1.553e+04 -30.164 < 2e-16 ***
## sqft_living 1.895e+02 3.826e+00 49.523 < 2e-16 ***
## bathrooms -1.463e+04 3.885e+03 -3.766 0.000167 ***
## grade 9.875e+04 2.495e+03 39.585 < 2e-16 ***
## view 6.851e+04 2.668e+03 25.684 < 2e-16 ***
## waterfront 5.615e+05 2.172e+04 25.853 < 2e-16 ***
## bedrooms -2.800e+04 2.400e+03 -11.667 < 2e-16 ***
## floors -2.461e+04 3.948e+03 -6.234 4.64e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 232300 on 17283 degrees of freedom
## Multiple R-squared: 0.5901, Adjusted R-squared: 0.5899
## F-statistic: 3554 on 7 and 17283 DF, p-value: < 2.2e-16
From above summary, we can say R-square is 59.72% or about 59.72% of variation in prices is explained by our chosen variables. Let’s work on increasing the accuracy of model by eliminating bedrooms and floors.
finalModel2 <- lm(price~sqft_living + bathrooms + grade + view + waterfront, data=trainingHouseData)
vif(finalModel2)
## sqft_living bathrooms grade view waterfront
## 3.279054 2.447752 2.482267 1.303474 1.210474
Again, all the vif values are less than 5. So, we incorporate all the variables.
step(finalModel2)
## Start: AIC=427451.8
## price ~ sqft_living + bathrooms + grade + view + waterfront
##
## Df Sum of Sq RSS AIC
## 9.4132e+14 427452
## - bathrooms 1 3.8429e+12 9.4516e+14 427520
## - waterfront 1 3.7003e+13 9.7832e+14 428116
## - view 1 3.9994e+13 9.8131e+14 428169
## - grade 1 9.5435e+13 1.0368e+15 429120
## - sqft_living 1 1.3552e+14 1.0768e+15 429775
##
## Call:
## lm(formula = price ~ sqft_living + bathrooms + grade + view +
## waterfront, data = trainingHouseData)
##
## Coefficients:
## (Intercept) sqft_living bathrooms grade view
## -548057.1 175.7 -30342.4 99983.0 72120.9
## waterfront
## 567935.6
The equation in this case becomes price = 178.1(sqft_living) – 29722.6(bathrooms) + 98868.0(grade) + 70679.4(view) +588863.0(waterfront)-544112.4. Let’s now find out the R square of this model.
summary(finalModel2)
##
## Call:
## lm(formula = price ~ sqft_living + bathrooms + grade + view +
## waterfront, data = trainingHouseData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1200221 -125937 -18891 97404 4857478
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.481e+05 1.390e+04 -39.44 <2e-16 ***
## sqft_living 1.757e+02 3.522e+00 49.88 <2e-16 ***
## bathrooms -3.034e+04 3.612e+03 -8.40 <2e-16 ***
## grade 9.998e+04 2.388e+03 41.86 <2e-16 ***
## view 7.212e+04 2.661e+03 27.10 <2e-16 ***
## waterfront 5.679e+05 2.179e+04 26.07 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 233400 on 17285 degrees of freedom
## Multiple R-squared: 0.5861, Adjusted R-squared: 0.586
## F-statistic: 4896 on 5 and 17285 DF, p-value: < 2.2e-16
As you can see, the R square is nearly the same but our model has less variable dependency now. Also, since the P value of all the variables is less than 0.05, we reject the null hypothesis that there is no relationship among a particular variable and price and accept the alternate hypothesis that the price is dependent upon all the given variables. Now, let’s see if the assumptions of linear regression are satisfied or not.
library(lmtest)
## Loading required package: zoo
##
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
par(mfrow=c(2,2))
plot(finalModel2)
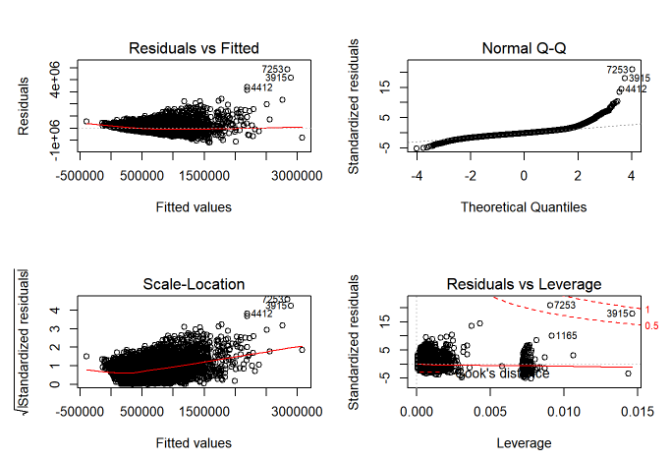
According to the assumptions of linear regression, these graphs must be uniformly distributed but that is not so here. So, we need to improve our model. Let’s now use our second model to predict the price for test dataset.
quantile(trainingHouseData$price, seq(0, 1, 0.01))
## 0% 1% 2% 3% 4% 5% 6%
## 75000.0 153000.0 175000.0 190954.4 202500.0 210000.0 219970.0
## 7% 8% 9% 10% 11% 12% 13%
## 226465.0 234000.0 240000.0 246000.0 250000.0 255000.0 260000.0
## 14% 15% 16% 17% 18% 19% 20%
## 266500.0 270975.0 276000.0 280000.0 287000.0 291510.0 299000.0
## 21% 22% 23% 24% 25% 26% 27%
## 300000.0 306500.0 311925.0 317000.0 322000.0 325000.0 330000.0
## 28% 29% 30% 31% 32% 33% 34%
## 335000.0 340000.0 346000.0 350000.0 355000.0 360000.0 365042.0
## 35% 36% 37% 38% 39% 40% 41%
## 370975.0 375000.0 380500.0 388500.0 394905.0 399950.0 402000.0
## 42% 43% 44% 45% 46% 47% 48%
## 410000.0 415000.0 420000.0 425000.0 430000.0 436000.0 440000.0
## 49% 50% 51% 52% 53% 54% 55%
## 449000.0 450000.0 458000.0 465000.0 470000.0 475799.4 483972.5
## 56% 57% 58% 59% 60% 61% 62%
## 490000.0 499000.0 501000.0 510000.0 520000.0 525000.0 533040.0
## 63% 64% 65% 66% 67% 68% 69%
## 540000.0 548000.0 550060.0 560000.0 569000.0 575555.0 585000.0
## 70% 71% 72% 73% 74% 75% 76%
## 595000.0 603500.0 615000.0 625000.0 635000.0 645000.0 654000.0
## 77% 78% 79% 80% 81% 82% 83%
## 665000.0 678020.0 690000.0 700500.0 718500.0 732000.0 749997.8
## 84% 85% 86% 87% 88% 89% 90%
## 762000.0 780000.0 799080.0 815000.0 838000.0 860000.0 889000.0
## 91% 92% 93% 94% 95% 96% 97%
## 917450.0 950000.0 994970.0 1059800.0 1150000.0 1250000.0 1378600.0
## 98% 99% 100%
## 1595000.0 1959100.0 7700000.0
As you can see, there are outliers in the above price variable. So, we need to perform outlier handling.
trainingHouseData_new = trainingHouseData
trainingHouseData_new$price = ifelse(trainingHouseData_new$price>=1959100.0, 1959100.0, trainingHouseData_new$price)
trainingHouseData_new$price = ifelse(trainingHouseData_new$price<=155000.0, 155000.0, trainingHouseData_new$price)
finalModel3 <- lm(price~sqft_living + bathrooms + grade + view + waterfront+ bedrooms + floors, data=trainingHouseData_new)
summary(finalModel3)
##
## Call:
## lm(formula = price ~ sqft_living + bathrooms + grade + view +
## waterfront + bedrooms + floors, data = trainingHouseData_new)
##
## Residuals:
## Min 1Q Median 3Q Max
## -970881 -120334 -19718 90945 1220350
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.662e+05 1.327e+04 -35.144 < 2e-16 ***
## sqft_living 1.465e+02 3.268e+00 44.822 < 2e-16 ***
## bathrooms -1.608e+04 3.318e+03 -4.847 1.26e-06 ***
## grade 1.026e+05 2.131e+03 48.145 < 2e-16 ***
## view 6.690e+04 2.278e+03 29.362 < 2e-16 ***
## waterfront 3.265e+05 1.855e+04 17.602 < 2e-16 ***
## bedrooms -1.567e+04 2.049e+03 -7.644 2.22e-14 ***
## floors -1.479e+04 3.372e+03 -4.386 1.16e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 198400 on 17283 degrees of freedom
## Multiple R-squared: 0.6047, Adjusted R-squared: 0.6046
## F-statistic: 3778 on 7 and 17283 DF, p-value: < 2.2e-16
Thus, the R square has improved to 61.07%. Let’s now do the assumptions analysis.
par(mfrow=c(2,2))
plot(finalModel3)
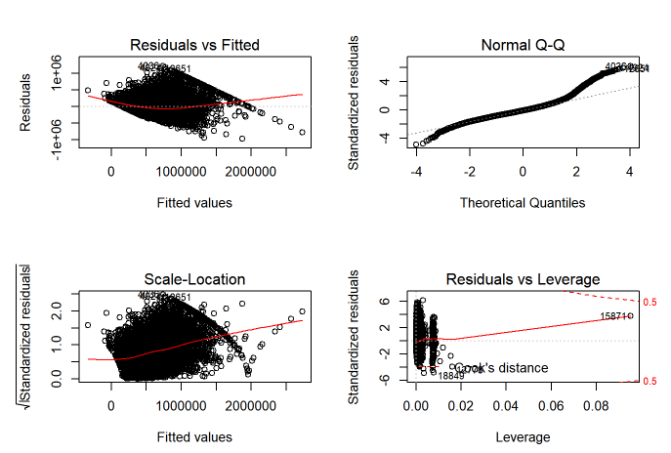
Thus, with outlier manipulation, the residuals vs leverage quality has dropped but quality for other graphs has improved. Also, now 61.07% of variation in price can be explained by the other independent variables in the model. Let’s now apply durbin watson test to our model.
durbinWatsonTest(finalModel3)
## lag Autocorrelation D-W Statistic p-value
## 1 0.0131114 1.973754 0.09
## Alternative hypothesis: rho != 0
The DW statistic is 1.978 or approximately 2. Thus, there is no autocorrelation among the variables. Hence, all the assumptions of linear regression are satisfied.
hist(residuals(finalModel3))
 The histogram of residuals is also coming out to be approximately normal which is a positive indication.Now, let’s check for homoscedasticity.
The histogram of residuals is also coming out to be approximately normal which is a positive indication.Now, let’s check for homoscedasticity.
plot(trainingHouseData_new$price, residuals(finalModel3))

The distribution is uniform in nature which is another positive indication. Now, let’s do the prediction.
testHouseData$predictedPrice = predict(finalModel3, testHouseData)
Please Write Your Comments.
Thanks,
Rakesh Kumar















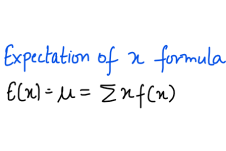











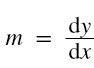 and in case of multiple input variables or features,
and in case of multiple input variables or features,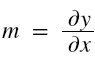

 is done to overcome the problem of cancellation of positive values with negative values of errors upon addition.
is done to overcome the problem of cancellation of positive values with negative values of errors upon addition.